Binary Search

One method of searching through a data structure, such as an array, is iterate through each element of the structure until the desired element is found. This method is known as a linear search.
In some scenarios, it is wasteful to visit every element of a data structure to locate a particular element. A binary search removes some of this overhead by halving it’s search range until the element is located. A binary search requires the structure being searched is sorted.
Binary Search Tree
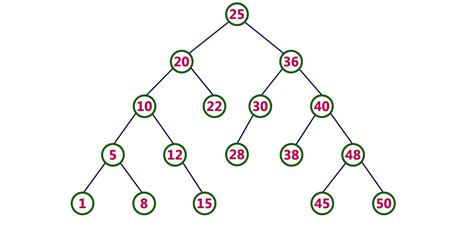
A binary search tree (BST) is a data structure consisting of a single ‘root’ node and any number of internal nodes. Each node contains a pointer to a left subtree and a pointer to right subtree. A BST follows the property that the key value of each node of the left subtree is less than the key value of the root node, and the key value of each node of the right subtree is greater than the key value of the root node. Because of this property, each comparison allows approximately half of the remaining tree to be skipped when searching for a key value.
A BST allows binary search for looking up, adding, and removing items
Time Complexity in Big O Notation
| Algorithm | Average | Worst Case |
|---|---|---|
| Space | O(n) | O(n) |
| Search | O(log n) | O(n) |
| Insert | O(log n) | O(n) |
| Delete | O(log n) | O(n) |
Nodes
At the most basic level, a node is structure that contains a key value and a pointer to it’s own left subtree and a pointer to it’s own right subtree
Searching
A BST can be searched iteratively or recursively
The pseudo code for searching a BST is as follows:
// point to root of bst
Node* nodePtr = root;
// while nodeptr isn't null
while(nodePtr){
// key found, return node ptr
if(key==nodePtr->key)return nodePtr;
// key greater, search right
if(key>nodePtr->key)nodePtr=nodePtr->right;
// key less, search left
else nodePtr=nodePtr->left;
}
return nodePtr;
Inserting
Inserting a new node into a BST is accomplished with the following routine:
- Create a new node
- Locate appropriate position for new node
- Point parent node to new node
The pseudo code for inserting a new node is as follows:
// point to root of bst
Node* nodePtr = new Node(keyValue);
if(root==nullptr)root = nodePtr;
else{
Node* tmp = root;
while(tmp){
if(tmp->key > keyValue){
// if left node is available, place new node here
// if not, search left
}
else
// if right node is available, place node here
// if not, search right
}
}
Deleting
In order to remove a node from the BST, the node must be deleted and any pointers referencing the node must be updated.
While removing a node from a BST, the underlying structure of the BST must be retained. This may require updating the removed node’s parents and children. This is summarized in the following 3 cases:
- The removed node has no children
- The removed node has either a left child or a right child (1 child)
- The removed node has both a left child and a right child (2 children)
No Children
The most straight forward case. The node’s parent’s pointers need to be disassociated from the node being deleted.
bool BST::noChildren(Node *node, Node *parent) {
if (node->left == nullptr && node->right == nullptr) {
// node being removed is the root of the BST
if (parent == nullptr) {
root = nullptr;
}
// node being removed is a left child
if (parent->left == node) {
parent->left = nullptr;
}
// node being removed is a right child
else
parent->right = nullptr;
return true;
}
// node has atleast one child
return false;
}
One Child
When deleting a node that has one child, the parent’s pointer needs to be updated to point to what the child is currently pointing to.
bool BST::oneChild(Node *node, Node *parent){
// node being removed has right child
if (node->right!=nullptr && node->left==nullptr) {
// node being removed is root
if(parent==nullptr){
root=node->right;
}
// node being removed is parent right child
else if(parent->right==node){
parent->right = node->right;
}
// node being removed is parents left child
else
parent->left=node->right;
return true;
}
// node being removed has left child
else if (node->right==nullptr && node->left!=nullptr){
// node being removed is root
if(parent==nullptr)root=node->left;
// node being removed is parents right child
else if(parent->right==node)parent->right=node->left;
// node being removed is parents left child
else parent->left=node->left;
return true;
}
return false;
}
Two Children
The third case can be confusing. The goal is to keep the underlying structure a binary tree.
A common approach is to locate the smallest value contained in the node’s subtree. This node will be put where the current node is located, and it is referred to as the successor node.
Locating the successor done by traversing the entirety of the node’s left subtree. While moving down the subtree, a record must be kept of the previous node visited, the successor node’s parent.
Once the lowest node is located, it is handled by one of the above two functions (no children or two children). This node is going to be put where the node being deleted is presently located, so it must be deleted from it’s current position. Finally, the successor is updated to point at the deleted node’s children.
void BST::twoChildren(Node *node, Node *parent){
Node* successor = node->right;
Node* prev = node;
// find the smallest key in this nodes left subtree
while(successor->left!=nullptr){
prev = successor;
successor = successor->left;
}
// check if lowest key node has no children or one child
if(!noChildren(successor, prev)){
oneChild(successor, prev);
}
successor->left = node->left;
successor->right = node->right;
if(parent==nullptr)root=successor;
else if(parent->right==node)parent->right = successor;
else parent->left = successor;
return;
};