Djikstra’s Shortest Path
Background
The purpose of Djikstra’s shortest path algorithm is to determine the shortest distance between the root node and all other nodes. Distance may not be the best term. The value associated with edges of the graph need not be distance. They could be costs associated following a given path, or the number of other entities traversing the given path at the same time. The point is that all of the edges have values associated with them, and the goal is to make it to any given node while minimizing the value associated with getting there.
Example Graph
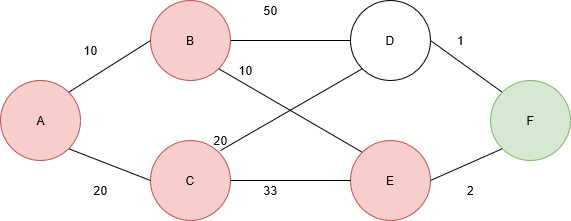
This is the graph used for this example:
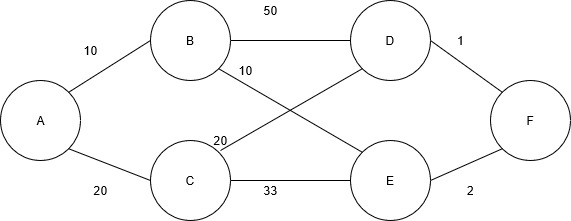
Method
The process involves creating a list of unvisited nodes. For this example, the unvisited set includes {A, B, C, D, E, F}. In order to track this list of unvisited nodes, a set of boolean values is used, and it is initialized in the following way:
pathSet = { false, false, false, false, false, false }
A seperate set of values is also needed for all the value associated with getting to a given node. This example uses node A as a starting point. The root node will have a value of 0 in this value set, and the remaining values will be set to some max value. The inital distance set is initialized in the following way:
distanceValues = { 0, max, max, max, max, max }
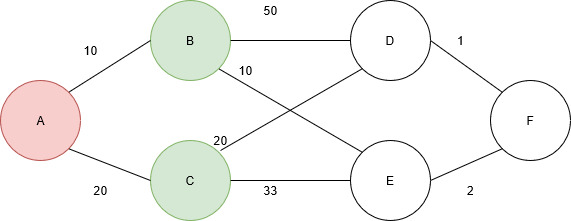
When node A is visited, it is removed from the unvisited list, and the weights associated with connected nodes are evaluated. Node A is connected to nodes B and C. The weights associated with B and C are 10 and 20. These values are added to the values set. The visited node set and the distance values are as follows:
pathSet = { true, false, false, false, false, false }
distanceValues = { 0, 10, 20, max, max, max }
Next, node B is visited. Node B is connected to A, D, and E. the values are 10, 50, and 10. The value added to the value set will now be the sum of the value associated with getting to B from A and then from getting to D and E from B. The value set now contains {0, 10, 20, 60, 20, inf}.
The visited node set and the distance values are as follows:
pathSet = { true, true, false, false, false, false }
distanceValues = { 0, 10, 20, 60, 20, max }
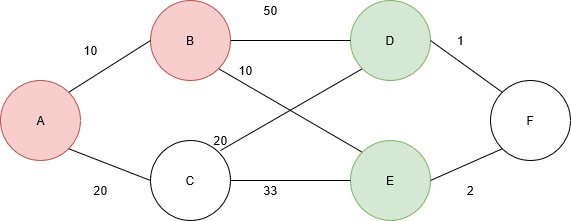
Next, node C is visited. Node C is connected to A, D, and E.
Node D and E already have distance values. The value associated with travelling to node E from C is greater than the current distance value, but this is not the case for travelling from node D from node C.
The visited node set and the distance values are as follows:
pathSet = { true, true, true, false, false, false }
distanceValues = { 0, 10, 20, 40, 20, max }
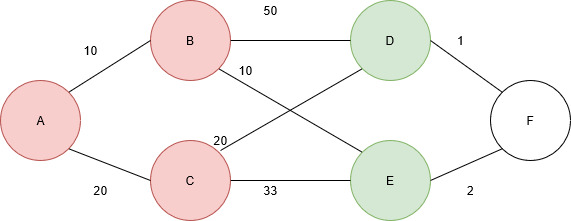
Next, node D is visited. Node D is connected to
 Here is the code to determine the next minimum distance to process
Here is the code to determine the next minimum distance to process
int findNextMinimumDistance(vector<int> &distanceVector, vector<bool> &pathSet){
// initialize minimum value to large number
int min = INT_MAX;
int minIndex;
// check for each node in shortest path set
for(int i = 0; i < NUM_VERTICES; i++){
// if node does not exist in the shortest path set and the distance value for this node is less than the current minimum value
if(pathSet[i] == false && distanceVector[i] <= min){
// updated minimum to this value
min = distanceVector[i];
// update minimum index to this index
minIndex = i;
}
}
return minIndex;
}
Initially, the ‘pathSet’ vector contains a false entry for each node. The ‘distanceVector’ vector contains 0 for the first node, and a set max value for all other nodes.
pathSet = { false, false, false, false, false, false }
distanceVector = { 0, max, max, max, max, max }
the function iterates through all values in distance vector and path vector. If the path vector contains a false value at a given index, the node has not been visited. If the ‘distanceVector’ entry is less than the max value, it means that a minimum value path has been determined for this node.
Again, the first node processed is node 0, which is the only position in the distance vector that contains a value less than the max value, forcing it to be processed first. The initial call to this function returns the index of 0, which corresponds to node A.
As the graph is processed, this function will chose the next node to process based on the value associated with that node in the distance vector.
Here is the code that processed the nodes of the graph:
for(int j = 0; j < NUM_NODES - 1; j++){
// find shortest path to un visited nodes
int shortestIndex = findNextMinimumDistance(distanceVector, pathSet);
// update visited node list
pathSet[shortestIndex] = true;
for(int k = 0; k < NUM_NODES; k++){
if(!pathSet){
if(thisGraph[shortestIndex][k]){
if(distanceVector[shortestIndex] != INT_MAX){
if(distanceVector[shortestIndex] + thisGraph[shortestIndex][k] < distanceVector[k])
distanceVector[k] = distanceVector[shortestIndex] + thisGraph[shortestIndex][k];
}
}
}
}
The first step is to find the next shortest path index in line. After determining which node will be visited next, the ‘pathSet’ value for the next node is set to true, which removes it from consideration when processing the other nodes.
After the shortest index is set, all the nodes of the graph are considered. In order for the distance vector to be updated, a few requirements need to be met.
First, the node can’t have already been processed by the algorithm. If the pathSet value for a given node is true, the distance vector entry for this node has already been determined.
The next condition is that an edge from the current node to a given a node exists. If it doesn’t, there is no use in considering it for a shortest path candidate.
Additionally, the shortest path to the current node must have already been computed in order for the paths computed with respect the current node to have any meaning.
Finally, if the distance vector entry for the current node plus the path to the next node is less than the current recorded shortest distance for the next node, the distance value is updated