Dynamic Programming
Dynamic programming is a description of a programming method which uses previously computed results to obtain current results.
Any solution that depends upon a previous solution, or could be returned by a formulaic alteration to an existing solution, is a candidate for dynamic programming. A common example is a function to determine the nth value of the fibonacci sequence.
The fibonacci sequence is the set of numbers whose values are determined by the sum of the previous two numbers in the set, excluding the first two numbers in the set. For example, the first eight numbers of the fibonacci sequence are:
| 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 |
This set is frequently used as a primer for recursive functions. When solving for the nth number recursively, the solution looks like:
int fibb(int pos){
if(pos==0)return 0;
if(pos==1)return 1;
return fibb(pos-1) + fibb(pos-2)
}
The 0th and 1st elements of the fibonacci sequence are base cases, set at 0 and 1.
This function will call recursively until either of the base cases are met. Here is how the function call graph looks for recursively determining the 5th number in the fibonacci sequence.
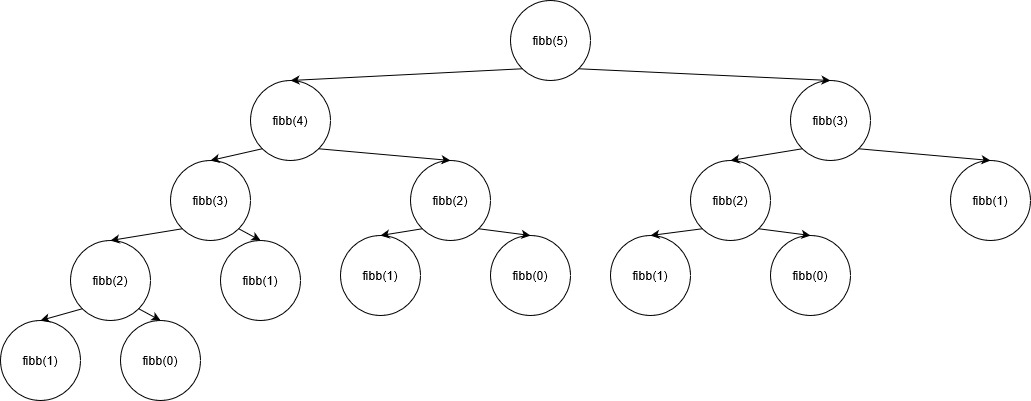
The repeated calculations that produce the same result can be costly. All recursive functions suffer from this potential limitation.
The results of the calculations could instead be stored in an array, saving some of the overhead. It should be noted that while this can save some performance overhead, dynamic programming does increase the storage overhead of a routine.
Solving the fibonacci sequence with dynamic programming would look like the following:
int dp[MAX];
void initDP{
dp[0] = 0;
dp[1] = 1;
for(int i = 2; i < MAX; i++){
// init dp array to negative one, indicating this solution hasn't been generated yet
dp[i] = -1;
}
}
int fibb(int pos){
if(dp[pos]==-1){
return dp[pos] = fibb(pos-1) + fibb(pos-2);
}
else return dp[pos];
}
This function still works recursively, but removes the need to calculate the same solution multiple times.
Dynamic programming comes in two main flavors. They are top down and bottom up.
Top down
The fibonacci function is an example of a top down dynamic programming. The function works from the current position towards the base case, generating any new solutions as needed. This is very similar to the recursive solution, except the return value is saved for later use.
The saving of the return value is known as memoization.
Bottom up
Alternatively, dynamic programming solutions can be derived from the bottom up. Instead of working towards the base case, the function can start at the base case and build towards the desired case. This is an iterative approach. Using the fibonacci sequence again, a bottom up approach would look like:
int dp[MAX];
dp[0] = 0;
dp[1] = 1;
for(int i = 2; i < desiredIndex; i++){
fibb[i] = fibb[i-2] + fibb[i-1];
}
Observation
The difficulty associated with dynamic programming is the intuition associated with identifying the pattern that generates the next iteration’s solution.
Common candidates for dynamic programming solutions include:
- Optimization problems
- Set problems
Example
The knapsack problem is a common optimization problem. Given a set of values, an associated set of weights, and a container that can only support a fixed maximum weight, find the set that would sum to maximum value.
For example, given the following value/weight sets:
Values: 60, 100, 120
Weights: 10, 20, 30
and a max capacity of 50, what is the maximum subset of values such that the sum of their associated weights is less than or equal to the max capacity? The values are atomic, meaning they can not be taken partially. They either exist in the solution set or they don’t.
One approach to this problem is to view each value with respect to the values that are already known.
Instead of looking at the entire set, start with just the first value in the set.
If the question was to pick a single item with a weight less than 50, and there is only one choice, and that item has a value of 60, the solution is apparent.
Using this idea, a table of values can be built. The number of rows in the table is determined by the number of items in the value set, and the number of columns in the table is determined by the given capacity, divided by the smallest weight. Since, the values are atomic, the columns of the table can only increase at the rate of the smallest weight (I’m not sure if this is true).
Here is a snippet of c++ that will be used to set the table up for this example:
// vector of values
vector<int> values = {60, 100, 120};
// vector of weights
vector<int> weights = {10, 20, 30};
// empty vector to hold capacities
vector<int> capacities;
// initialize a capacities vector
// the example is seeking the max value at capacity = 50, populate capacity vector with 0, 10, 20, 30, 40, 50
for(int i = 0; i < 6; i++){
capacities.push_back(10*i);
}
// create the table, which is a vector of vectors
// values.size() = number of rows (3)
// capacities.size() = number of columns (6)
vector<vector<int>> dp(values.size(), vector<int>(capacities.size()));
The complete table, for reference purposes:
| 0 | 10 | 20 | 30 | 40 | 50 | |
|---|---|---|---|---|---|---|
| 60(10) | 0 | 60 | 60 | 60 | 60 | 60 |
| 100(20) | 0 | 60 | 100 | 160 | 160 | 160 |
| 120(30) | 0 | 60 | 100 | 160 | 180 | 220 |
Looking at the first row of the table, which contains the maximum value associated with choosing one item, the maximum value is 60. This table stops at 50, but if the capacity is any value greater than or equal to 10, the maximum value will still be 60.
This first row is an initialized row. The values in this row are not generated by the same algorithm that determines the rest of the table
Here is a snippet for generating this row:
for(size_t i = 0; i < capacities.size(); i++){
// compare capacity with weight of item. If weight is greater or equal, set value in table equal to value of item
if(capacities[i]>=weights[0]){
dp[0][i] = values[0];
}
}
In the second row of the table, choices now include value 1 and value 2. While the number of choices has increased, this has no impact on the maximum value until the capacity is equal to the weight associated with the second value. Even with two choices, the maximum value possible while the capcity is less than or equal to 10 is the value associated with single item used before.
When the capacity reaches 20, which is the weight of the second item, a decision must be made. Include the item or not. There is a value associated with each choice, so both outcomes need to be computed and compared.
If the item is included, the maximum value at this capacity will be this item’s value and whatever other items can exist in the container in addition to this item.
This highlights the functionality of the table. The maximum value at any previous capacity with out the current item has already been determined. The only action necessary is to determine the location of that result in the table. The table is organized by capacity, so the target value is located at the index of the capacity after the current items weight has been deducted from it. If the current item is included, which has a weight of 20, then the capacity is reduced by 20, making the remaining capacity 0. Referencing the table, the maximum value with respect to the previous item at this capacity is 0. If this item is included, it will be the only item in the container, and the value of the container will be 100.
If this item is not included, the max value that the container can have is the same value of the container determined for the previous item, which is 60.
Comparing these two values (60 and 100), the choice should be to select this item.
This pattern is repeated for the remaining entries in the table. Here is a loop that accomplishes this:
// i,j = row,col
// start at 1 for both -> row 0 has already been set (single item case), col 0 has already been set (0 capacity case)
for(size_t i = 1; i < values.size(); i++){
int currentItemWeight = weights[i];
for(size_t j = 1; j < capacities.size(); j++){
int valueA = 0, valueB = 0, currentKnapsackCapacity = capacities[j];
if(currentItemWeight <= currentKnapsackCapacity){
// this is only valid for this weight/capacity relationship.
int colIndex = (currentKnapsackCapacity - currentItemWeight)/10;
// include this item
// the value will be this items value + the maximum determined value at this capacity prior to this item
valueA = values[i] + dp[i-1][colIndex];
}
// exclude this item
valueB = dp[i-1][j];
dp[i][j] = max(valueA, valueB);
}
}