Graph Traversal
Concept
Graph traversal is the method with which a graph is iterated through. There are two primary methods: Depth First Search (DFS) and Breadth First Search (BFS).
DFS
DFS uses some data structure to track the nodes that have been visited. Each node may have multiple exit paths, and multiple exit paths may lead to the same node. In order to avoid visiting the same node multiple times, a record must be kept of where the graph traversing function has been and where it still needs to go.
There are both iterative and recursive methods for performing a depth first search on graph. This description outlines a recursive approach.
For a recursive approach, there are multiple methods for tracking the progress of the DFS function. This example will use a vector of boolean values to record which nodes have been visited and which haven’t. This vector is initialized to contain all false values each time the DFS function starts.
When each node is visited, the node’s that are pointed to by the path(s) out of the current node will be referred to as ‘discovered’. The same node can be discovered by multiple other nodes, but the node will only be visited if it hasn’t been visited before.
The graph is represented using a vector of vectors. Each node has a vector, and each node’s vector indicates if there is an edge from the given node to the other nodes in the graph.
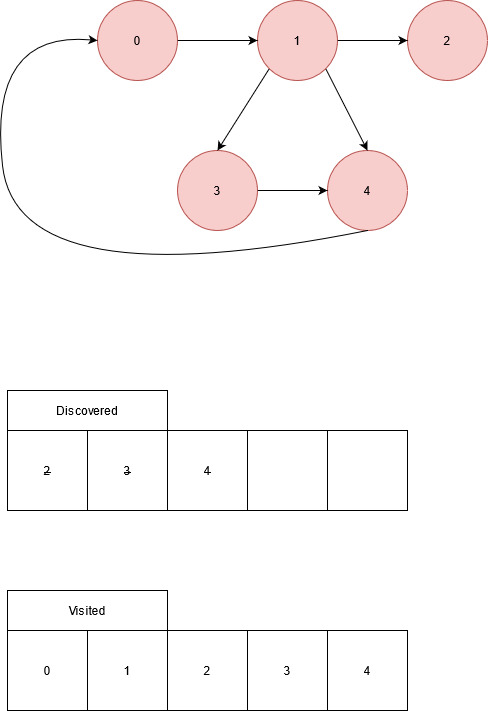
The following graph is used for this example:
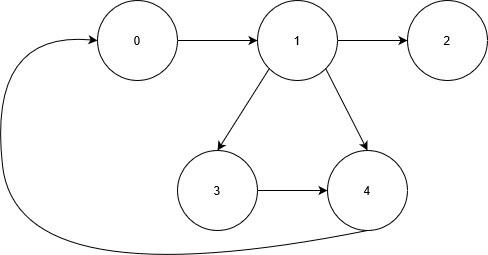
When laid out as a table, this is how the example graph is represented:
| 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 | 1 |
| 2 | 0 | 0 | 0 | 0 | 0 |
| 3 | 0 | 0 | 0 | 0 | 1 |
| 4 | 1 | 0 | 0 | 0 | 0 |
DFS works by recursively visiting the nodes that are connected to the current node.
Here is an example implementation of a recursive DFS function:
void dfs(int targetNode) {
boolVisited[targetNode] = true;
vector<int> currentNodeAdjacenyList = adjacencyList[targetNode];
for(int i = 0; i < numberOfNodes; i++){
// if there is a an edge from the current node to some other node, and the other node has not been visited, visit it
if(currentNodeAdjacenyList[i] && !boolVisited[i]){
dfs_b(i);
}
}
}
If DFS was executed on node 0:
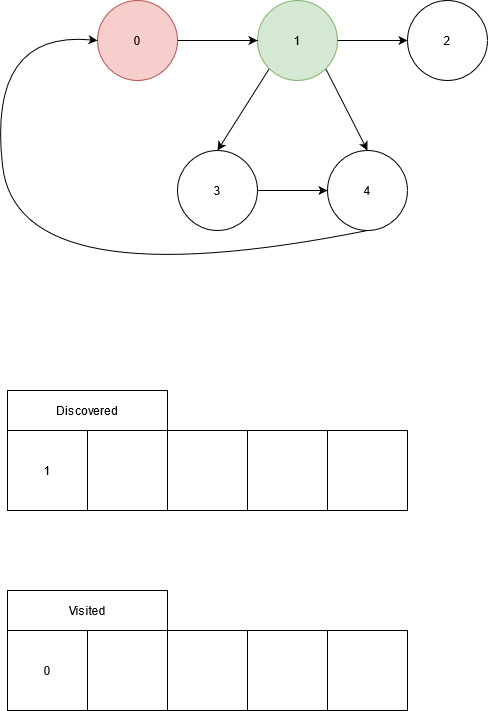
The adjacency list of node 0 is iterated through. Each entry in the adjacency list that isn’t set to 0 is checked against a list of nodes that have been visited. If the node has not been visited, the process is repeated on the unvisited node.
Unvisited: 1, 2, 3, 4 Adjacency list of node 0: 0, 0, 1, 0, 0
Edge from node 0 to node 1, node 1 is not visited. Visit node 1.
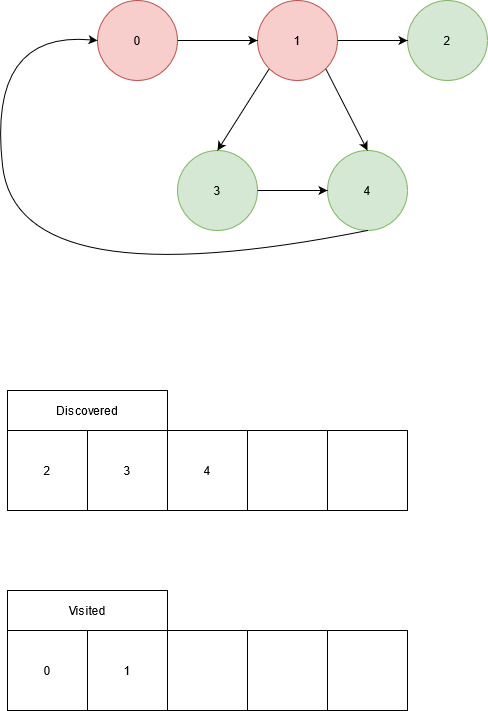
Unvisited: 2, 3, 4 Adjacency list of node 1: 0, 0, 1, 1, 1
Edge from node 1 to node 2, node 2 is not visited. Visit node 2.
Unvisited: 3, 4 Adjacency list of node 2: 0, 0, 0, 0, 0
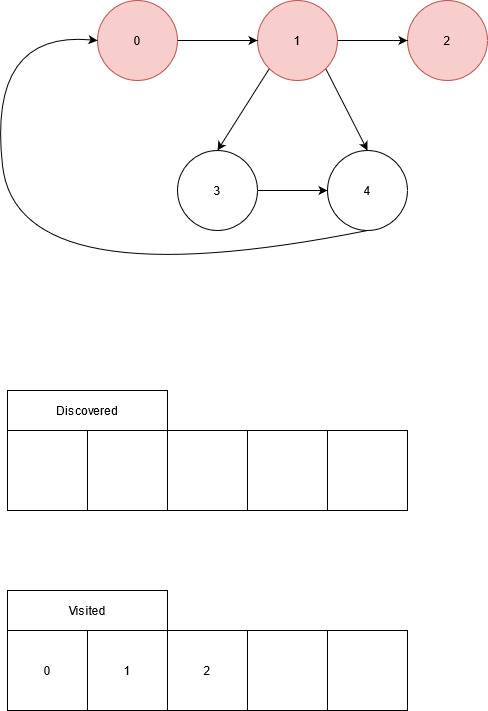
No edges exiting node 2, return to adjacency list of node 1.
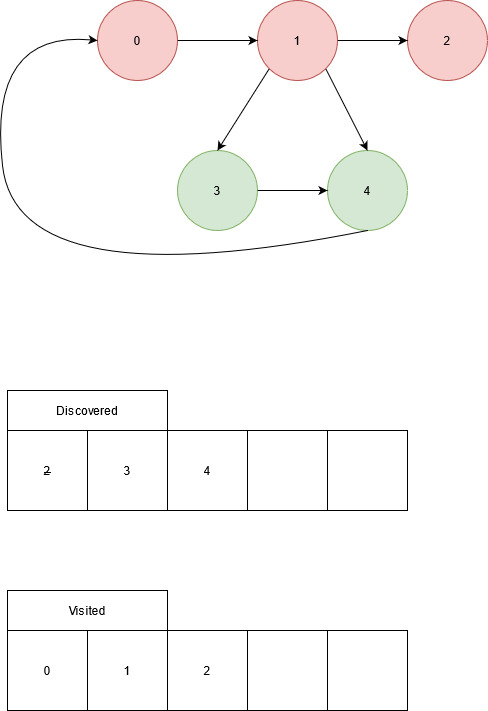
Unvisited: 3, 4
Edge from node 1 to node 3, node 3 has not been visited. Visit node 3.
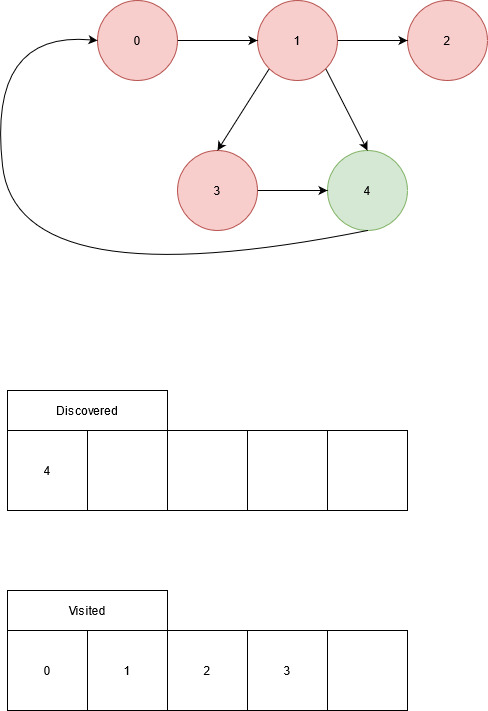
Unvisited: 4 Adjacency list of node 3: 0, 0, 0, 0, 1
Edge from node 3 to node 4, node 4 has not been visited. Visit node 4.
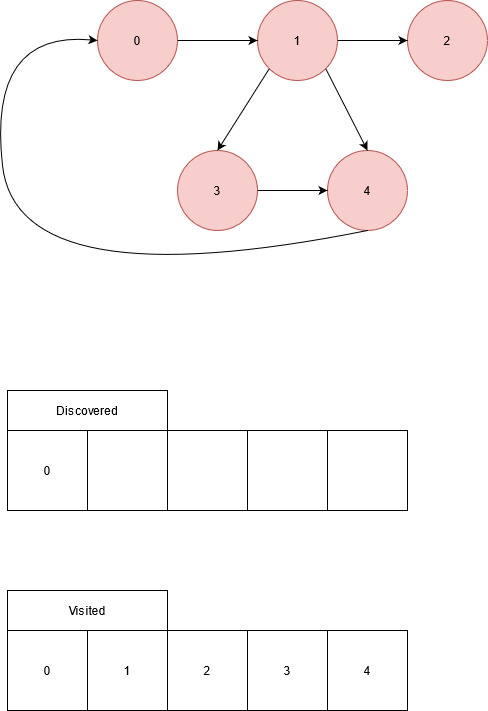
Unvisited: - Adjacency list of node 4: 1, 0, 0, 0, 0
Edge from node 4 to node 0, node 0 has been visted. No other edges from node 4, return to node 3’s adjacency list.
No other edges from node 3. Return to node 1’s adjacency list
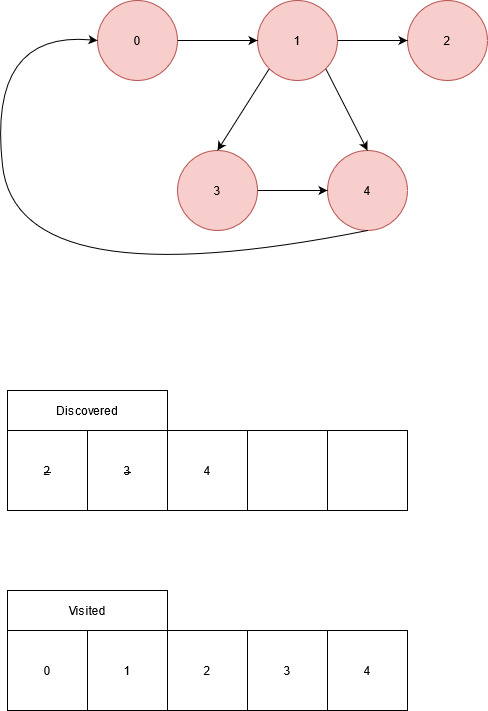
Edge from node 1 to node 4. Node 4 has been visted. No other edges from node 1. Return to node 0.
No other edges from node 0, return.
Detecting Cycles
DFS can be modified to detect cycles in a graph. A cycle is when a path creates a loop.
In order to detect a path, the nodes that have been visited during a given iteration through the graph need to be stored. This is different than tracking some shared structure that contains visit information. Discovering a node twice doesn’t equate to locating a cycle. Since the above DFS implentation is recursive, the function can be extended to update a ‘cycle’ vector each time the DFS function is called.
The cycle vector sets the visited nodes entry to true upon entry into the DFS function, and sets it back to false when exiting the function.
The downside of this method (at least the way I implemented) is that it only locates the longest cycle. The graph has a shorter cycle of node 0 -> node 1 -> node 4 -> node 0, but since node 4 is visited in node 3’s recursion, it isn’t re-visited by node 1’s recursion, which stops the shorter path from being identified as a a cycle.
What I have done to print shorter cycles in this scenario is store the node that has a back edge. The DFS function now checks if nodes within a given nodes adjacency list are back edges. If they are back edges, the current path is used a cycle, with the back edge node appended to it. This allows the cycle to be caught, even if the back edge node isn’t visited.
Here is the code:
void dfs(int targetNode) {
boolVisited[targetNode] = true;
boolCycle[targetNode] = true;
vector<int> currentNodeAdjacenyList = adjacencyList[targetNode];
for (int i = 0; i < numberOfNodes; i++) {
// if there is a an edge from the current node to some other node, and the
// other node has not been visited, visit it
if (currentNodeAdjacenyList[i] && !boolVisited[i]) {
dfs_b(i);
}
// if there is an edge from the current node to some other node, and the
// other node *has* been visited
else if (currentNodeAdjacenyList[i] && boolVisited[i]) {
// if the current node has been visited during the current path
// traversal, and the current node is not the
vector<int> thisCycle;
if (i != targetNode && boolCycle[i]) {
cout << "Back edge from node " << targetNode << " to node " << i
<< endl;
backEdges.push_back(targetNode);
// a cycle has been found
for (int j = 0; j < numberOfNodes; j++) {
// for all nodes in this cycle, add to a temp cycle list
if (boolCycle[j])
thisCycle.push_back(j);
}
// add front node to back, for clarity while printing
thisCycle.push_back(thisCycle[0]);
// add this cycle to collection of cycles
cycleList.push_back(thisCycle);
thisCycle.clear();
}
if (i != targetNode && isBackEdge(i)) {
cout << "Current node " << targetNode
<< " has path to known back edge (" << i << ")" << endl;
for (int j = 0; j < numberOfNodes; j++) {
if (boolCycle[j])
thisCycle.push_back(j);
}
// add back edge src node to cycle
thisCycle.push_back(i);
// add front node to back, for clarity while printing
thisCycle.push_back(thisCycle[0]);
cycleList.push_back(thisCycle);
thisCycle.clear();
}
}
}
// remove this node from cycle candidacy
boolCycle[targetNode] = false;
}
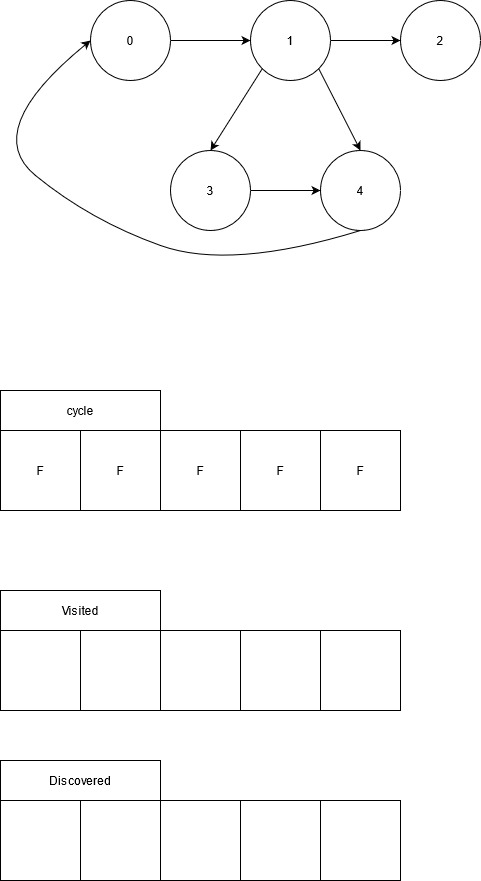
All of the nodes are indicated as non visited and none of the nodes are included in the current path
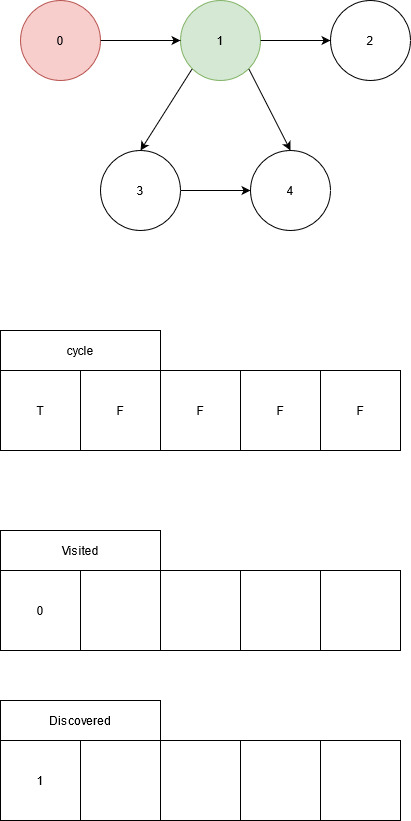
Node 0 discovers node 1, node 0 is added to the current path. Node 1 is visited.
Node 1 discovers nodes 2, 3, and 4. Node 1 is added to current path. Node 2 is visited.
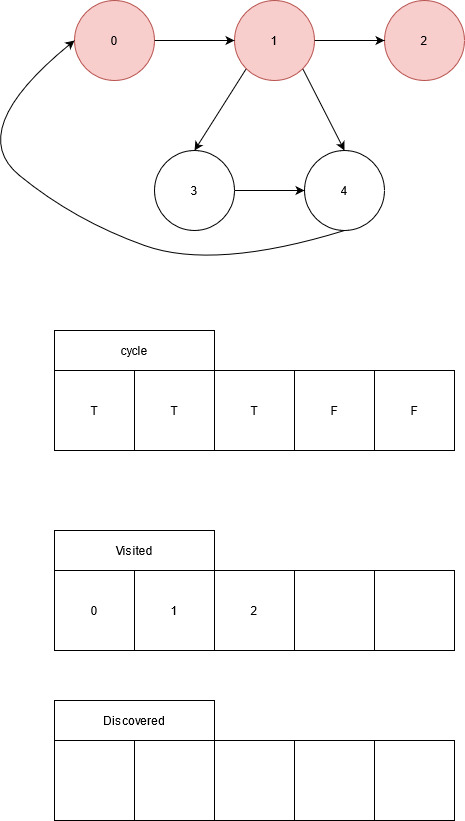
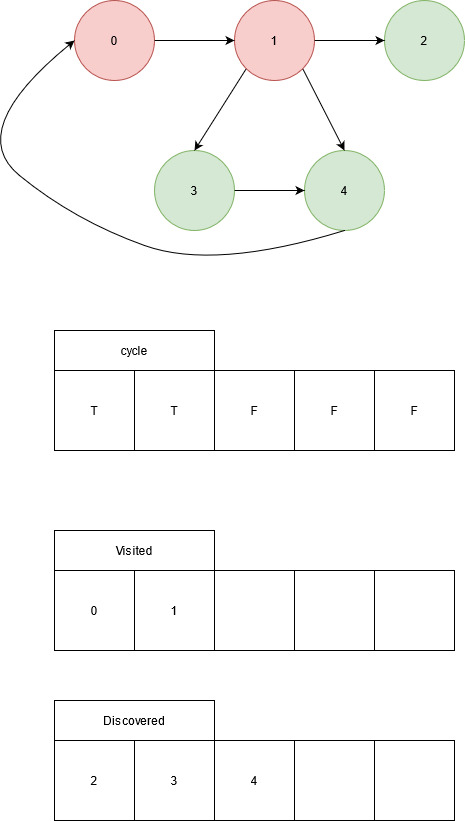
Node 2 doesn’t discover any nodes. Remove node 2 from the current path and return to node 1.
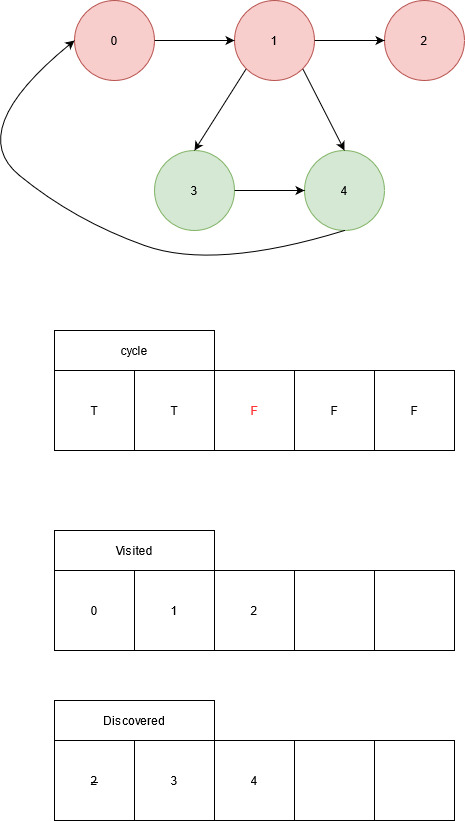
Visit node 3.
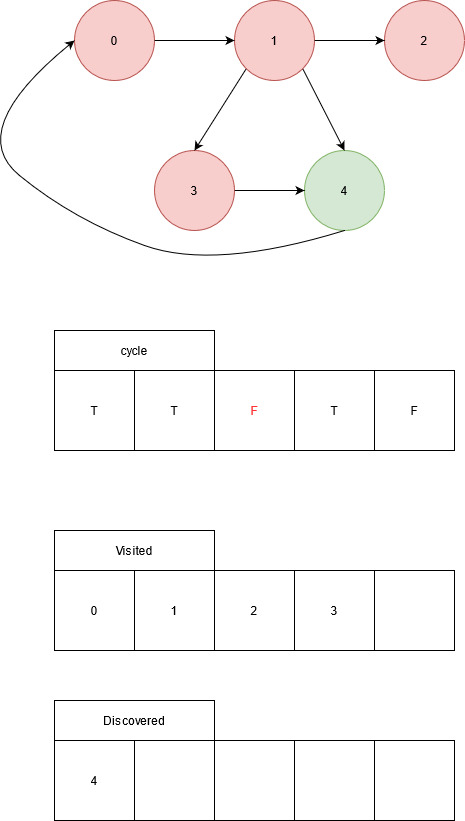
Node 3 added to the current path, node 3 discovers node 4. Visit node 4.
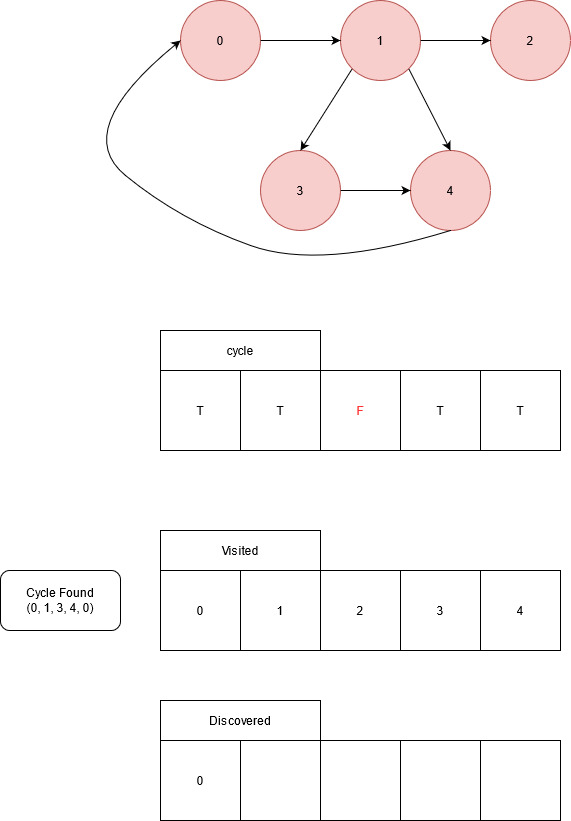
Node 4 discovers node 0. Node 0 is indicated in the current path. A cycle has been detected. No other nodes are discovered, return to node 3.
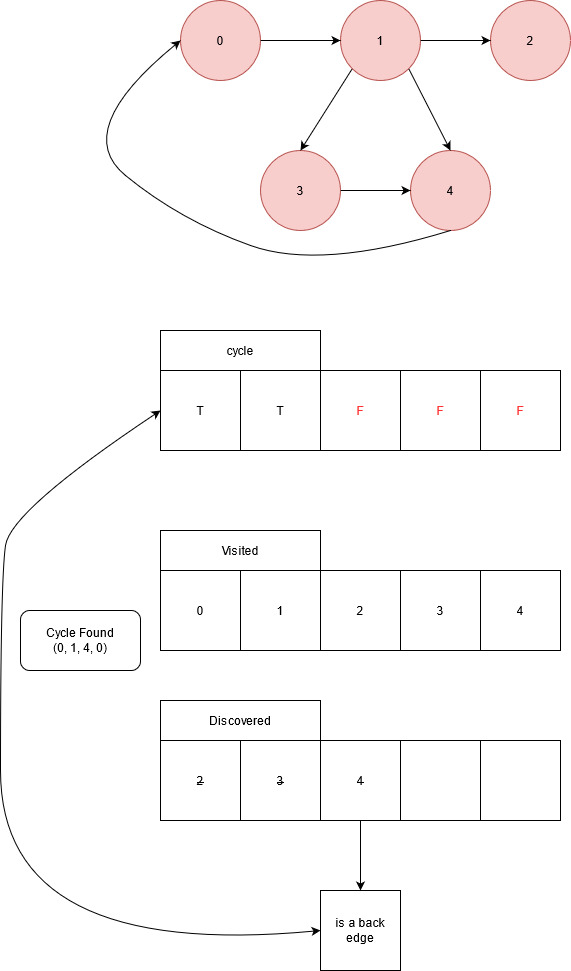
Node 3 doesn’t discover any other nodes, return to node 1. Node 1 identifies node 4, which has already been visited, as a back edge. A shorter cycle is discovered.