Hashing

At it’s highest level, hashing is the act of associating some value with some other value. Hashing as a concept occurs in the realm of cryptography, with a heavy focus on developing secure and efficient functions for the association of data with a particular key. That topic is outside of the scope of this project. Here, I will focus on the basics of hashing in order to implement a hash table.
An effective hashing function has the following parameters:
- Creates a reasonably unique key for each element
- Computes quickly
To be considered a perfect hash function, the function must generate a unique key for each element of the data set being hashed.
Division Method
Let’s say we have a known number of integer elements in a set of data. We could generate a key for each element by doing something like:
int key = value % numberOfElements;
If the data set contained 15 elements, the following values would produce the following keys:
| Value | Key |
|---|---|
| 10 | 5 |
| 16 | 1 |
| 12 | 3 |
Multiplication Method
A key can be generated by a multiplicative function. An example of this is:
int key = floor(n((value*a)%1))
where both n and a are both some constant values between 0 and 1
Mid Square Method
The mid sqaured method consists of squaring the value of the element being inserted and using the middle n digits of the result as the key, where n is the number of memory locations in the table.
For example, if the table had 1000 slots, the mid square function would return the middle 3 digits
Got stuck here thinking about how to extract three middle digits from an integer without creating a vector or string
Hash Table
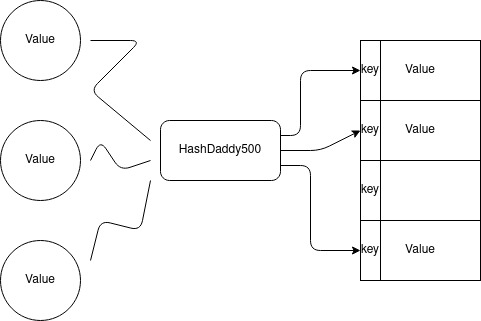
Hashing is used as a building block for the hash table data structure. A hash table consists of elements indexed by their key. This has an advantage over a simple array in terms of search time. Since the location of the element within the structure is dependent on the element, searching does not need to be iterative or binary. In a perfect hash table, an element can be found in constant time.
A hash table is built by allocating a fixed amount of contiguous memory, just like an array. When adding elements to the array, a hash function generates a key for the value, and the value is inserted into the allocated space at the index provided by the key.
If it is known that the allocated memory is greater than the required memory for the elements and the hash function generates a unique key for every value in the set, no further action is needed. If either one of those conditions is not met, a collision policy must be establised. A collision is when the index, produced by the key, points to a location in memory that is occupied with data. There are two primary choices for handling collisions:
- Probing
- Chaining
Probing handles a collision by iterating through the indices of the allocated memory
Load Factor
The load factor of a hash table is the ratio of the number of occupied slots ‘o’ and the number of available slots ‘a’
load factor = o/a
for example, a hash table with 75 occupied entries and 100 available entries has a load factor of .75
Time Complexity of Hash Tables
| Algorithm | Average | Worst Case |
|---|---|---|
| Space | O(n) | O(n) |
| Search | O(1) | O(n) |
| Insert | O(1) | O(n) |
| Delete | O(1) | O(n) |
Inserting
Inserting elements into a hash table is handled in two steps:
- Generating a key for the element
- Finding a location in the table to place to the element
If the hash table does not support collisions, attempting to insert at an index that contains data will result in returning a failure code.
Here is a snippet for a table insertion, with no collision policy. For this example, I have initialized all the elements in the table with a value of -1, indicating open slots.
bool insert(int value){
int key = hashFunc(value);
if(table[key]==-1){
table[key] = value;
return true;
}
return false;
}
If the table is configured for a probing policy, the insertion function would not return false until all slots were confirmed full.
Here is a snippet with probing:
bool insertCheck(int value){
int key, checkIndex;
key = hashFunc(value);
if(table[key]==-1){
table[key] = value;
return true;
}
else{
checkIndex = (key+1)%numberOfSlots;
while(checkIndex!=key){
if(table[chainIndex]==-1){
table[chainIndex] = value;
return true;
}
chainIndex=(chainIndex+1)%numberOfSlots;
}
}
return false;
}
Searching
Locating an element in hash table again involves generating the key for the element, and checking the table at the generated key’s index.