Insertion Sort
Insertion sort also has O(n^2) time complexity
Insertion sort advantages:
- More efficient in practice than other quadratic search functions, like selection sort
Insertion sort disadvantages:
- Inefficient on large lists
| Insertion Sort | Comparisons | Swaps |
|---|---|---|
| Worst-case performance | O(n^2) | O(n^2) |
| Best-case performance | O(n) | O(1) |
| Average performance | O(n^2) | O(n^2) |
How it works
Insertion sort works by checking behind the current index of the list while iterating. For each element in the list, the search checks from the curent elements index backwards until a value is found that is not greater than the current the element.
While values are found that are greater than the current element, the larger elements are pushed forward.
A common implementation consists of a while loop nested within a while loop. The outer loop moves forward through the elements, and the inner loop compares the current element with preceeding elements. Within the inner loop, if an element is found that is less than the current element, the values are swapped
Example
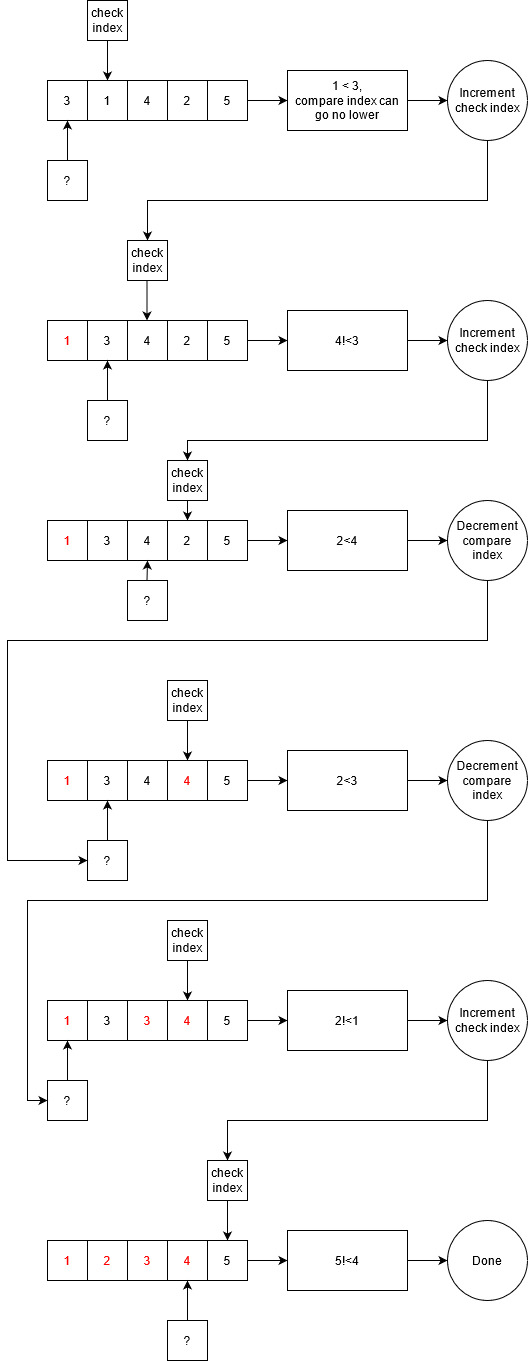
Pseudo Code
while( checkIndex < arrLength){
holdValue = values[checkIndex];
j = checkIndex - 1;
while( j >= 0 && values[j]>holdValue ){
values[j+1] = values[j];
j--;
}
values[j+1] = holdValue;
checkIndex++;
}
Advantage Versus Selection Sort
Insertion sort performs less comparisons based on the ‘sortedness’ of the data.
Disadvantage Versus Selection Sort
Insertion sort performs a greater number of swaps, so a greater number of memory writes. There are some scenarios where the designer may want to avoid this. For example, flash memory has a limited lifespan with respect to memory writes.