Merge Sort

Merge sort is a comparison based sorting algorithm, utilizing a divide and conquer method. Merge sort operates in O(n log n) run time, while both insertion sort and selection sort have O(n^2) run times. The reason that merge sort operates in O(n log n) time is that n comparisons are done for each division. Each division halves the previous division, so there are n comparisons that happen log(n) times.

The number of comparisons per sublist is proportional to the number of elements in the sublist, producing the ‘n’ factor of O(n log n). Since comparisons happen between sublists, and the number of sublists is the result of continually halving the original list, the amount of comparisons executed is only logarithmically proportional to the number of elements in original list, producing the log n factor of O(n log n).

Merge Sort
Best-case performance	O(n log n)
Worst-case performance	O(n log n)
Average performance	O(n log n)

Algorithm

• Divide unsorted list into sublists, each containing one element
• Compare elements in sublist a to element in sublist b
• Repeatedly merge sublists to produce new sorted sublists until only one sublist remains

High Level Description

Merge sort operates on the principle that a list with a single element is considered sorted. To that end, the merge sort algorithm repeatedly divides an array until it has arrived at a sublist with a single element. The single elements are compared and merged, until a sorted array is generated which contains all of the original elements.

Example

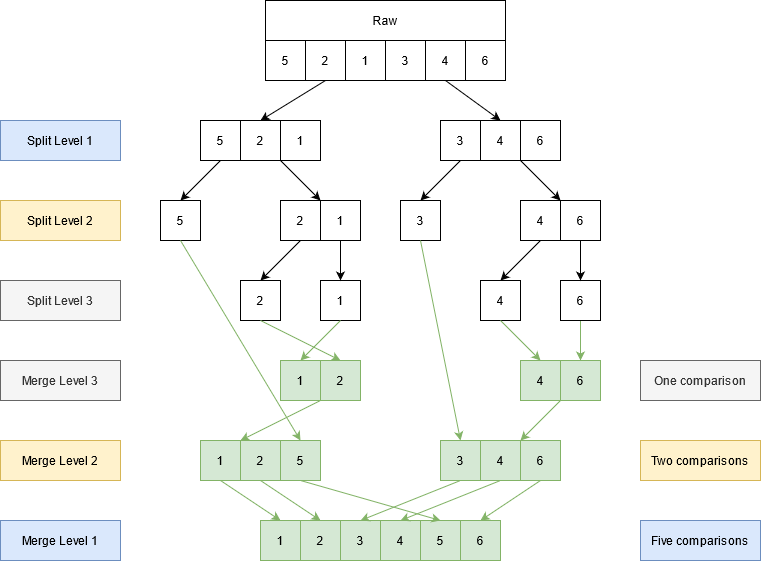
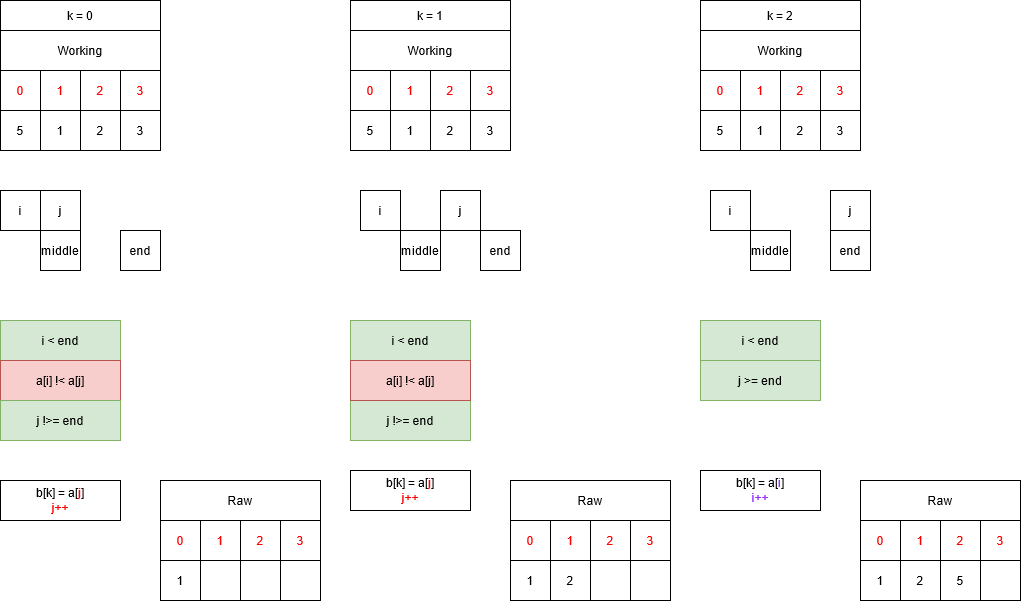
The above example uses the following list: 5,2,1,3,4,6

This list is passed as an argument to a recursive split function. The pseudocode for the split function is as follows:

void split(int a[], start, end, int b[]){
   if(end - start <= 1) return;
   int middle = (end + start)/2;
   split(b, start, middle, a);
   split(b, middle, end, a);
   merge(a, start, middle, end, b)
}

Where ‘a[]’ is the array containing the unsorted data, start and end are index references to the particular recursive iteration’s sublist, and ‘b[]’ is a dummy array, used for holding elements as needed.

Notice that the nested split calls swap the positions of ‘a[]’ and ‘b[]’. The reason is that a and b alternate between being used as containers for sorted and unsorted data. A diagram of the alternation, along with the recursive split calls is pictured below:

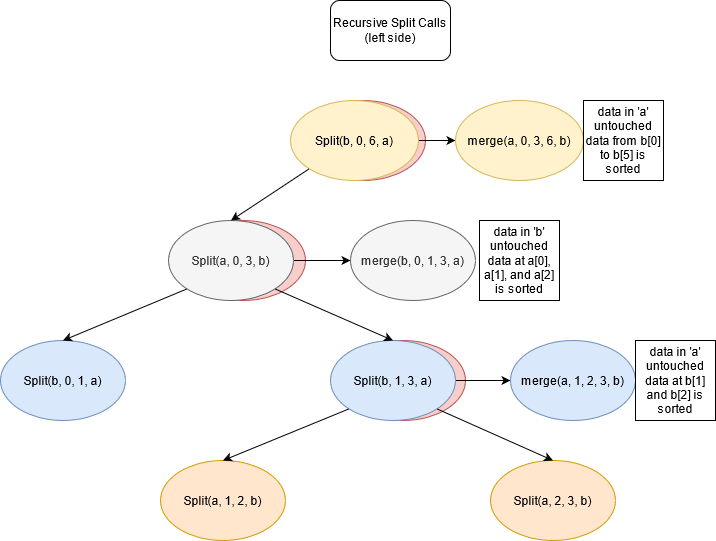
The first split call uses 0 and the length of the array as arguments for start and end, middle is set to 3((6 + 0)/2) and produces the following two sublists: 5,2,1 and 3,4,6

The split function prioritizes left recursion, and the second iteration of the split function uses the previously set ‘middle’ as it’s ‘end’ parameter.

The second split call produces the following two sublists: 5 and 2,1

Again, the left sublist is passed to the split function, but immediately returns due to conditional, which checks for a sublist of length 1.

After 2,1 is split to 2 and 1, the merge function located in the third split call is invoked. This merge operates on the single elements 2 and 1. These elements are sorted and placed in the ‘b[]’.

Here is the pseudocode for the merge function:

void merge(int a[], int begin, int middle, int end, int b[]){
    int i = begin, j = middle;
    for(int k = begin; k < end; k++){
        if( i < middle && (j >= end || (a[i] <= a[j]) )){
            b[k] = a[i];
            i++;
        }
        else{
            b[k] = a[j];
            j++;
        }
    }
}

In the merge call, ‘b[]’ is the destination array, ‘a[]’ is the source array, and beginning, middle, and end or used as to control the action taken in the for loop.

The element being copied to the destination array is either located at the i’th index of source array or j’th index of the source array.

i is initialized to point to the beginning of the left sublist being merged, and j is initialized to point to the beginning of the right sublist being merged.

k is initialized and bounded to be able to iterate through the entire range of the two sublists.

Note that the range of ‘k’ is exclusively less than the end value. The split and merge functions only operate on indices that are strictly less than this.

Here is a graphical representation of the logic:

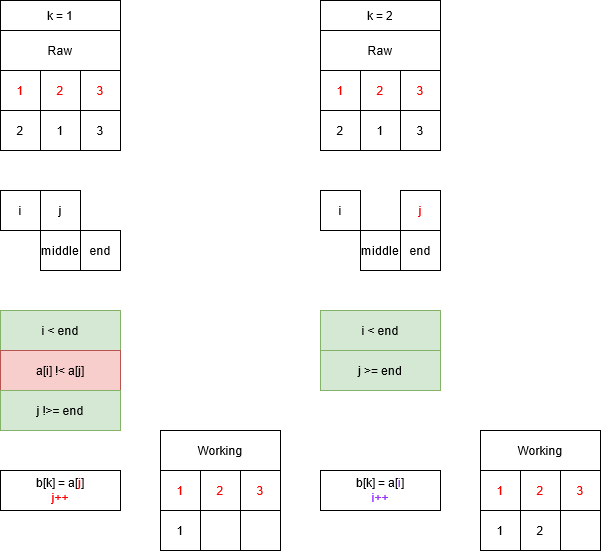
The merge call finishes the third split subroutine and the function returns to the second split function, which merges the sublist that was just sorted (1, 2) with the single element 5.

The flow of this merge is pictured below:

Code

Link to code