Selection Sort
Selection sort is a sorting method with O(n^2) time complexity.
Selection sort advantages:
- Simple
- In some scenarios, has a performance advantage over more complicated algorithms
Selection sort disadvantages:
- Inefficient on large lists
| Selection Sort | Comparisons | Swaps |
|---|---|---|
| Worst-case performance | O(n^2) | O(n) |
| Best-case performance | O(n^2) | O(1) |
| Average performance | O(n^2) | O(n) |
How it works
Selection sort works by treating the original list as two sub-lists. One sub-list contains the the original data, and one sub-list contains the sorted data.
The sub-list containing the sorted elements is populated by iterating through the unsorted list from a minimum index to the max index of list. The minimum index is updated on each pass through the unsorted list. Selection sort is an inplace sorting method, so no new memory is allocated during the search.
Example
Take the following list of integers as an example: 20, 12, 300, 3, 24
The following table shows the sub-lists after each iteration
| Unsorted | Sorted |
|---|---|
| (20, 12, 300, 3, 24) | () |
| (20, 12, 300, 24) | (3) |
| (20, 300, 24) | (3, 12) |
| (300, 24) | (3, 12, 20) |
| (300) | (3, 12, 20, 24) |
| () | (3, 12, 20, 24, 300) |
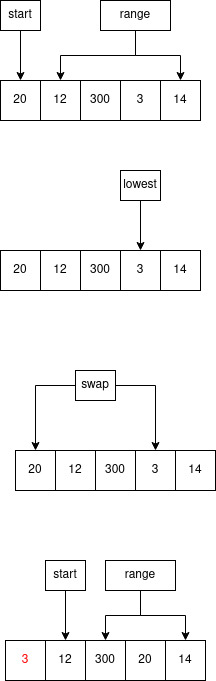
The typical implementation of selection sort is a nested loop, which results in O(n^2) time complexity. For each element in the list, the element is compared to the remaining elements in the list to determine the next lowest value.
The diagram below shows a single pass through a list
Pseudo code
int arrayLength = n;
int values[arrayLength];
int i, j, minIndex;
for(i = 0; i < arrayLength-1; i++){
minIndex = i;
for(j = i+1; j < arrayLength; j++){
if(values[j]<values[minIndex]){
minIndex = j;
}
}
if(minIndex != i){
swap
}
}
Advantage Versus Insertion Sort
Selection sort performs less swaps than insertion sort.
Disadvantage Versus Insertion Sort
Selection sort performs a greater number of comparisons than insertion sort. Insertion sort usually performs better.