Tries

A trie, also refered to as a digital tree or prefix tree, is a search tree used for locating specific keys from within a set. Keys are usually strings, and links between nodes are defined/referenced by single characters.

Nodes in a trie do not store a key value. Trie node’s are defined by their position with the structure.

Typical trie node’s have two primary components:

• Some structure containing pointers to the node’s children
• A marker designating node as leaf

A node’s children are stored as pointers in an additional data structure. The examples that I have found so far use a fixed sized array, with a lay out looking something like this:

class TrieNode(){
public:
// only used here to print the data
char data;
// matrix of pointers
TrieNode* children[n];
// bool value to determine if a given node is a leaf node
bool isLeaf;
};

An Example Use Case

What immediately comes to my mind when learning about tries is a dictionary. When I think about an entry in the dictionary, I think about it’s position relative to the entirety of the dictionary. I think that’s why most examples use an example with strings as the entry, and characters as the positional references. The prefixing that takes place in a dictionary is intuitive to me, so I am going to use that as a template.

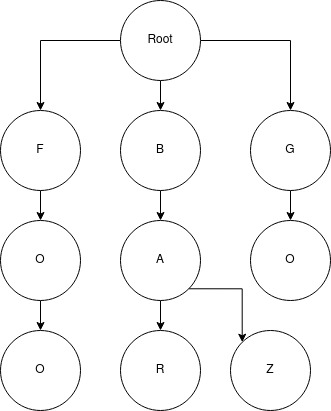
Let’s say I wanted to store a bunch of words in some program, I’m going to use a trie, and the first word I was going to add was ‘ark’. Because the trie is empty, I am going to be adding three nodes, a node representing each letter, pointing to the next letter in the word, until the last letter, which I will flag as the end of a word. Here’s a quick representation:

root node -> node containing a -> node containing r -> node containing k (flagged as end of word)

To accomplish this:

• A node for each letter is created
• Each node contains a pointer to the next letter in the word

Suppose I add another word, ‘arch’. In this case, I will only be adding two nodes, one for c and on for h.

root node -> node containing a -> node containing r -> (new) node containing c -> (new) node containing h (flagged as end of word)

To accomplish this, two things happened:

• Two new nodes were created
• The collection of pointers owned by the node that contains r is updated to now also point to c

If I were to add the word ‘bark’ to the structure, four nodes would be added. The idea of prefixing is important. For a given word, I only reference existing nodes until a novel character is introduced. If the first character of the string is not present in the pointer list of the root node, I need to start a new branch of the trie.

Structure

Here is the tree node structure:

class TrieNode {
  public:
  // actually containing data, for example purposes
    char data;
    // designator for end of a string
    bool isLeaf;
    // container for node's pointers
    TrieNode* children[NODECOUNT];
    // initializing the pointers
    TrieNode(char nodeData){
        this->data = nodeData;
        this->isLeaf = false;
        for(int i = 0; i < NODECOUNT; i++){
          this->children[i] = NULL;
        }
    }
};

Insertion

When a string is added to the trie, the characters of the string are used to traverse the content of the trie.

The root node pointer structure is checked for the first letter of the string. If present, the function moves to next letter of the string, and points to the node indicated by the root node’s pointer. This processed is looped for each letter of the string.

void Trie::insert(std::string thisString){
    // start at root
    TrieNode* curr = this->root;
    // index for checking current node's pointer array
    int idx;
    for(int i = 0; i < thisString.size(); i++){
    // set index to integer form of character
        idx = thisString[i] - 48;
        // if node does not exist, creat new node, move to new node
        if(!curr->children[idx]){
            curr->children[idx] = new TrieNode(thisString[i]);
            curr = curr->children[idx];
        }
    }
    // node associated with last letter of string marked as a leaf node
    curr->isLeaf = true;
}

Searching

Searching for a given string in the structure is similar:

bool Trie::searchTrie(std::string thisString){
    TrieNode* curr = this->root;
    int idx;
    for(int i = 0; i < thisString.size(); i++){
        idx = thisString[i] - 48;
        if(!curr->children[idx])
            return false;
        else curr = curr->children[idx];
    }
    return true;
}

Starting with the root node and the first character of the string, nodes are checked for the string contents. If at any point in the search, the current node doesn’t contain a pointer to the next letter, the search returns as false.

It the trie contained ‘arc’ and was searched for ‘ark’: root -> ‘a’ (exists) -> ‘r’ (exists) -> ‘k’ (doesn’t exist) fail return

Deletion

Deletion, which is handled recursively, can be a little tricky for tries. Here’s the process:

• Start at root, first character of string
• Check if depth is equal to length of string
• If depth is equal to string, remove node, move back up through trie
• If not move to next character in string

The depth parameter can only be incremented if the character is found in child pointer arrays.

Here is the code:

TrieNode* Trie::remove(TrieNode *currentNode, std::string thisString, int currentDepth){
    if(currentNode==NULL)return NULL;

    // if position in tree matches length of string
    if(currentDepth==thisString.size()){
        if(currentNode->isLeaf){
            currentNode->isLeaf = false;
        }
        if(emptyNode(currentNode)){
            delete(currentNode);
            currentNode = NULL;
        }
    return currentNode;
    }

    int idx = thisString[currentDepth] - 48;
    currentNode->children[idx] = remove(currentNode->children[idx], thisString, currentDepth++);
    if(emptyNode(currentNode)&&currentNode->isLeaf==false){
        delete(currentNode);
        currentNode = NULL;
    }
    return currentNode;
}

Code

Link to code